Research
Vahid Karimipour
Sharif University of Technology
Link to ArXiv
Google Scholar
Curriculum Vita
Our recent papers
Below you will find our papers in the last two years. In each case, you can read a summary of each paper which is different from the abstract of the paper. They will also show you a flavor of our current research interests. Click on the title of each paper which will direct you to the arXiv address of the paper where you can download the file of the paper and find the detailes of the published paper.

Protecting an unknown qubit state by weak measurement
O. Heibati, A. Mani, E. Faizi and V. Karimipour
Measurement collapses the state of a quantum system, but not always! We can look at a quantum state only gently so that its state does not collapse and is only slightly disturbed. In return we obtain little information about the quantum state. We use this technique to combat the decoherence of a large class of quantum channels which have one invariant pure state. What we do is to slighly project the state toward the invariant state of the channel and then after the channel we slightly retieve the the state again. The projecting and and retrieving of the state are done by weak measurements.

Quasi-inversion of quantum and classical channels in finite dimensions
F. Shahbeigi, K. Sadri, M. Moradi, K. Zyczkowski and V. Karimipour, J. Phys. A: Math. Theor. 54 345301 (2021)
We study classical and quantum stochastic processes in arbitrary dimensions. This is an extension of the work that the last author has done before for qubit channels in collaboration with Fabio Benatti and Roberto Floreanini, see Physical Review A 101, 032109 (2020). Contrary to qubit channels, this study is far from complete, particularly due to the lack of classification of quantum channels in higher dimensions and the very limited knowledge that is available on the extreme points of the set of these channels.

Simulating of X-states and the two-qubit XYZ Heisenberg system
on IBM quantum computer
Mahsa Karimi, Fereshte Shahbeigi and V Karimipour, Phys. Scr. 97 025101 (2022)
The IBM quantum computer offers a free platform consisting of 6 qubits for free which you can use for running your quantum algorithm and testing their results. You can also simulate your quantum algorithm by a classical computer called QISKIT and see how much the results of the real IBM quantum computer with its noisy gates differ from the simulated ones. We have used this platform for studying the entanglement properties of a large class of two qubit gates, called the X-states.
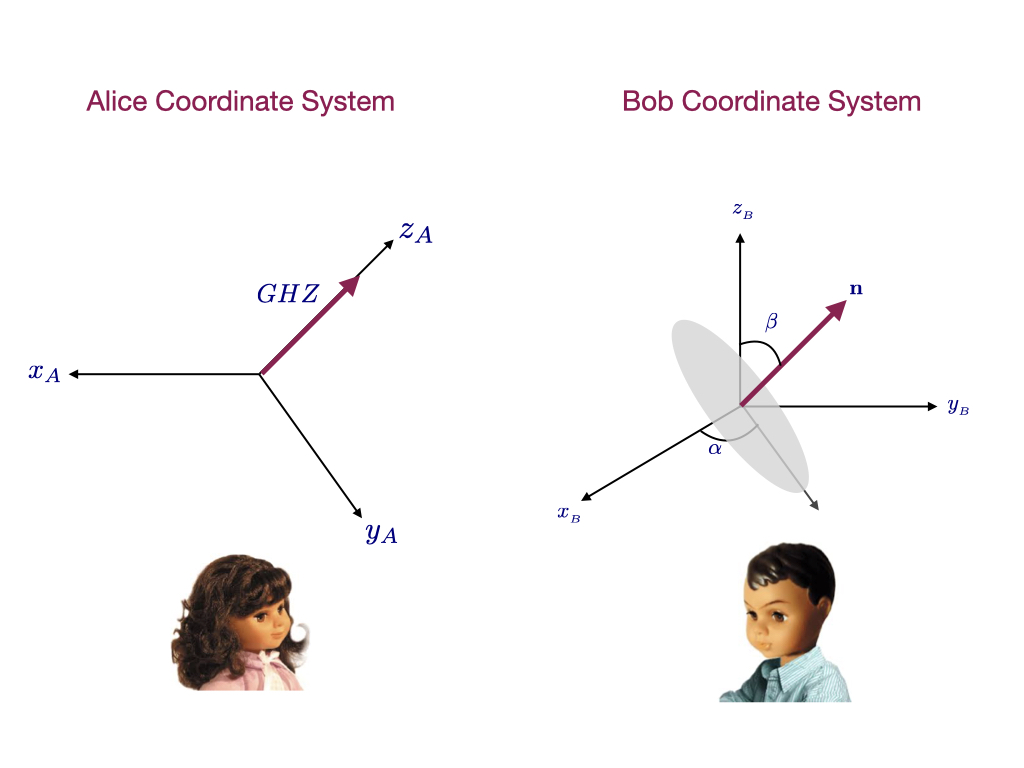
GHZ states as near-optimal states for reference frame alignment,
M. R. Koochakie, V. Jannessari and V. Karimipour, Quantum Information Processing ,10, (2021)
Alice is on Earth, Bob is in a space station. Their reference frames are misaligned. Alice wants to send a quantum state to Bob so that by measuring this state, he can find the orientation of Alice coordinate system. Which state is the best carrier of this information? By "best" we mean the precision (quantified by the quantum Fisher information) and the ease of measurement. We show that the best state is the GHZ state.
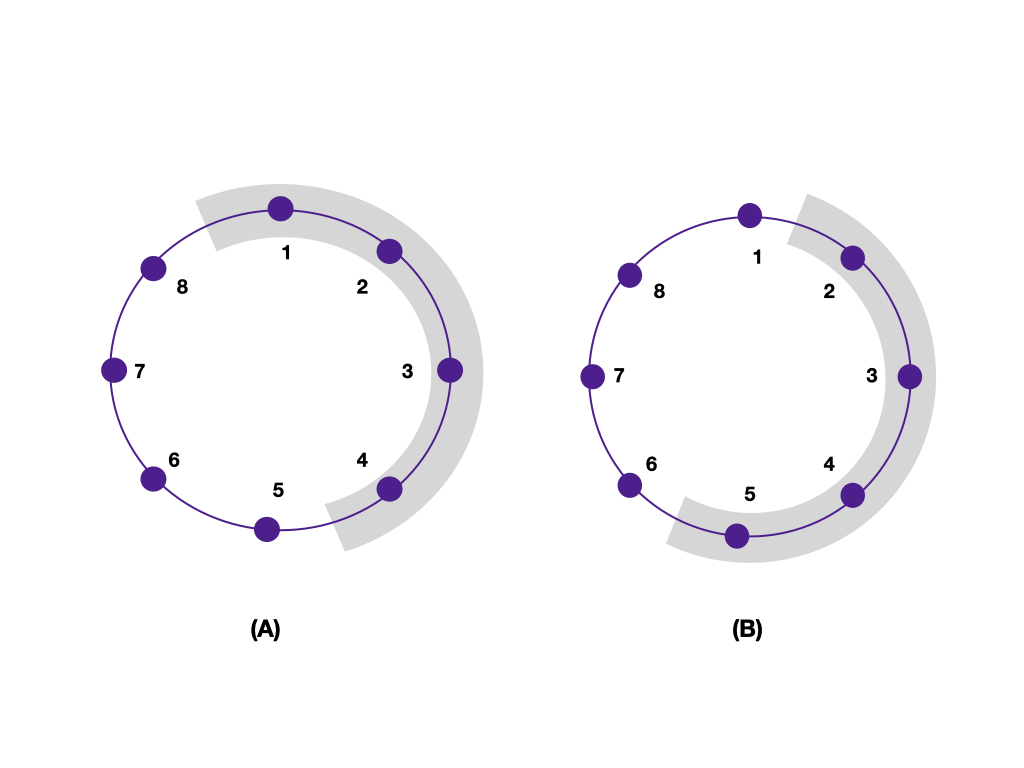
Planar maximally entangled states,
M. Doroudiani and V. Karimipour Physical Review A (2020).
A Bell state has the property that the reduced density matrix of each of the particles is maximally mixed, carrying no information at all for the person who posses this particle. Can this be generalized to many particles? For example, consider a state shared between say 4 persons so that any two of them see their share as a maximally mixed state, carrying no information at all. How about 6 persons or 8 person? How about particles which are adjacent to each other? We show that for adjacent particles, there is always a solution for any number of particles and for any dimension.
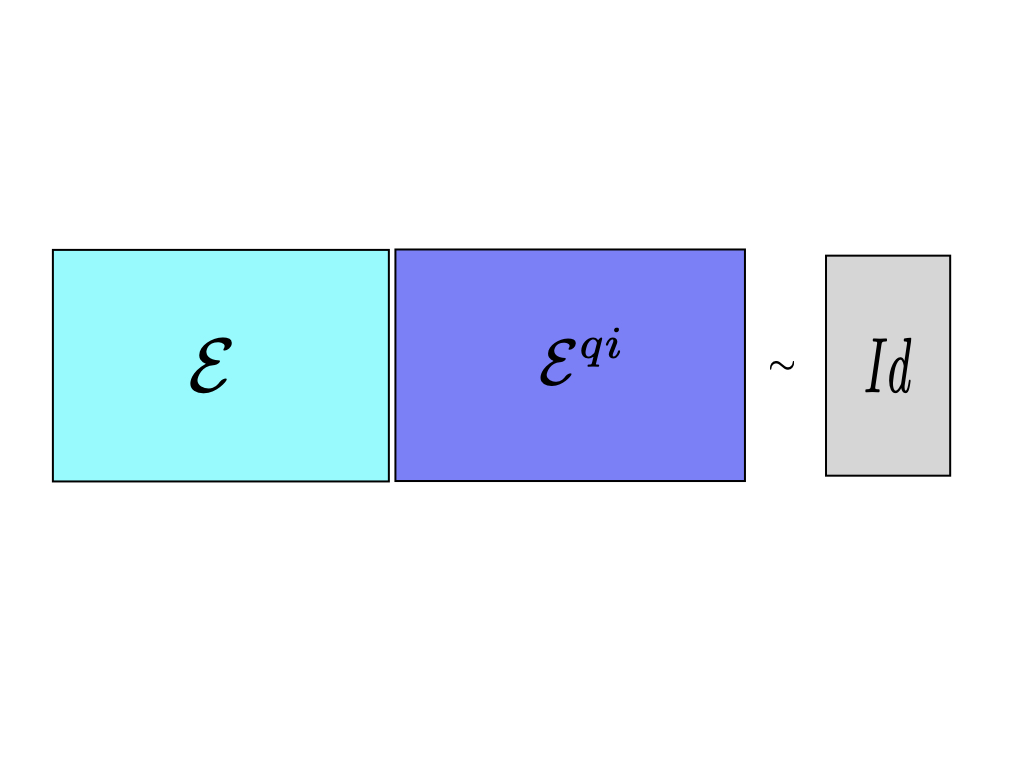
Quasi-inversion of qubit channels
V Karimipour, F. Benatti, R. Floreanini, Physical Review A (2020)
In general quantum operations, or quantum channels cannot be inverted by physical operations, ie, by completely positive trace-preserving maps. An arbitrary state passing through a quantum channel loses its fidelity with the input. Given a quantum channel E, we discuss the concept of its quasi-inverse as a completely positive trace-preserving map E^qi which when composed with E increases its average input-output fidelity in an optimal way. The channel E^qi comes as close as possible to the inverse of a quantum channel. We give a complete classification of such maps for qubit channels and provide quite a few illustrative examples.
Quantum key distribution with no shared reference frame,
F Rezazadeh, A Mani, V Karimipour, Quantum Information Processing (2020)
In the usual quantum key distribution systems, Alice and Bob should have a common reference frame. We show that even if they do not have a shared reference frame, i.e. when Alice is on Earth and Bob is in space, they still can share a secret key, provided that they use three photons instead of one photon for each bit of the key.

Entangled states as robust and re-usable carriers of information,
S Emamipanah, M Asoudeh, V Karimipour, Quantum Information Processing (2020)
Entanglement can be used in such a way it acts as a carrier of states from one place to another without itself being destroyed. This is much like the current classical communication lines, where information is uploaded at one point and downloaded in another point. During transmission the state is in a completely mixed state and carries no information if somebody have access to it.
Exact generation of quantum states by the dynamics of spin chains,
M. Moradi and V. Karimipour, Physical Review A (2019)
A spin chain with Heisenberg interaction can, by its natural dynamics, carry quantum states from one end of it to the other. Can we tune the couplings of the chain so that its natural dynamics evolves a single excitation on the left hand side to develop to an arbitrary state, i.e. a Guassian, or a W state on the whole chain?

Entanglement-assisted communication in the absence of shared reference frame,
A. Beheshti, S. Raeisi and V. Karimipour, Physical Review A (2019)
Alice wants to communicate a real number to Bob who is remote from him (deep in space) and whose coordinate system is not known to Alice. How Alice can communicate this real number? Shall she encode it in the angle between two spin 1/2 particles, or in an entangled state? We show that an entangled state is the better choice.
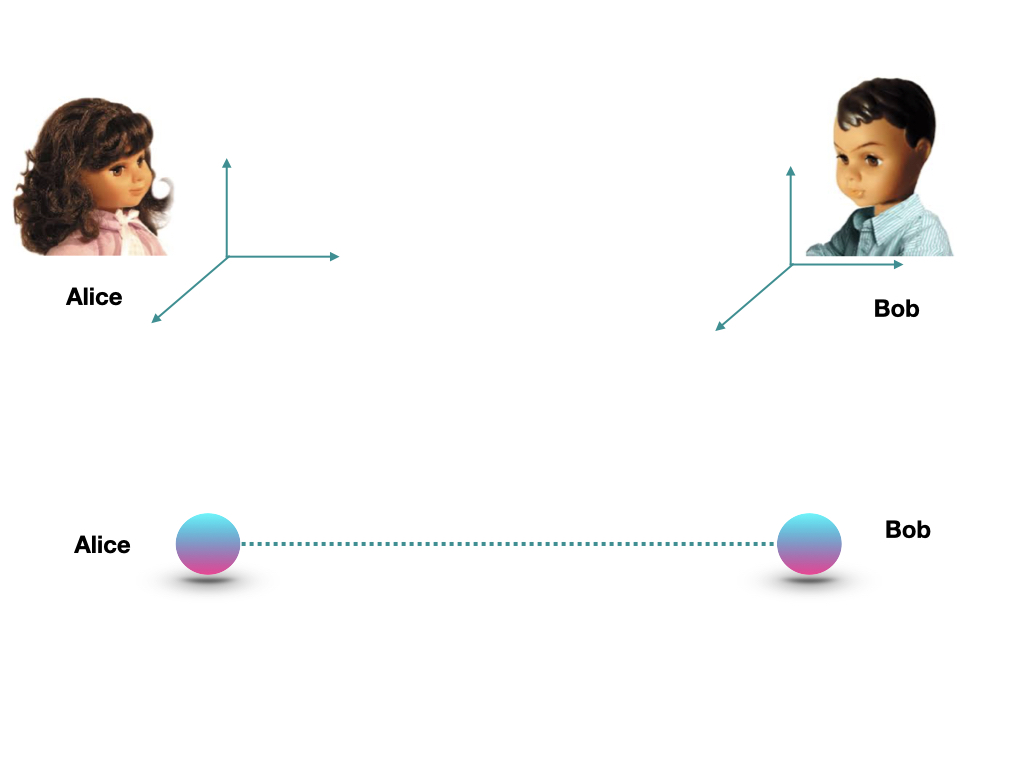
The power of a shared singlet state, compared with a shared reference frame,
F. Rezazadeh, A. Mani and V. Karimipour, Physical Review A (2019)
Alice and Bob can either share a Cartesian frame of reference or a maximally entangled state. Which resource should they choose? We show that depending on the task they want to perform, a maximally entangled state is their better option. We present three such tasks.
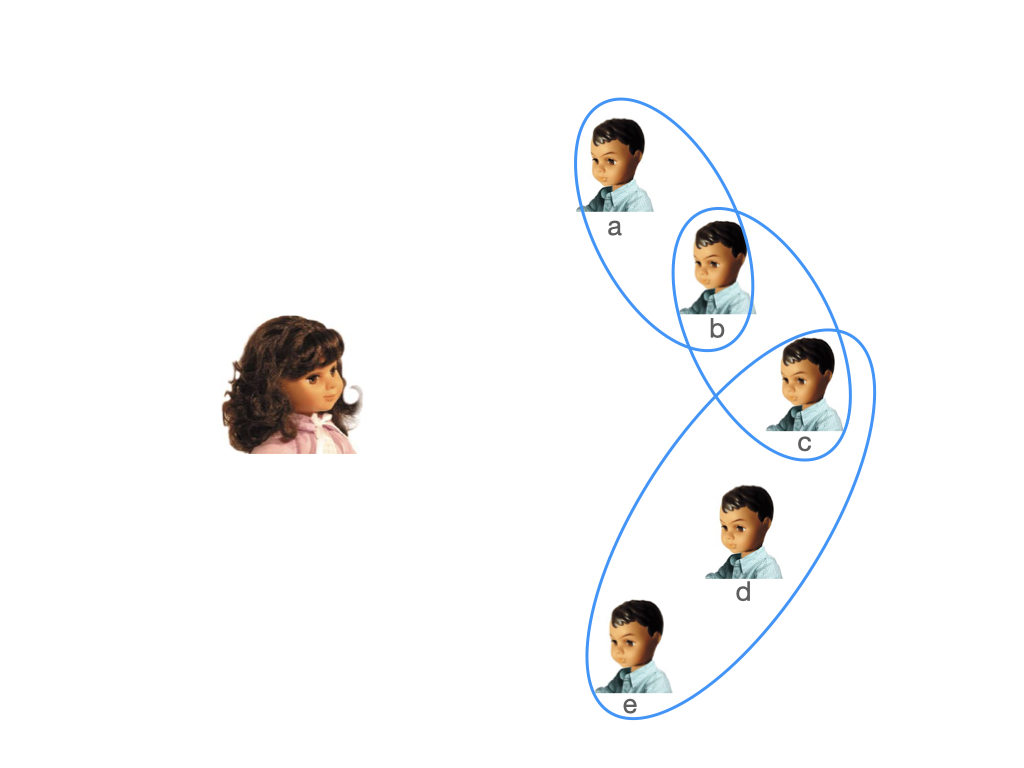
Computing on Quantum Shared Secrets for General Quantum Access Structures
Roozbeh Bassirian, Sadra Boreiri, and Vahid Karimipour, Quantum Information Processing (2019)
Alice wants to share a quantum state to a group of people so that they can retrieve it by collaboration among themselves, but all the receivers do not have the same level of authorization. Here the subsets (a,b), or (b,c) or (c,d,e) can, but other subsets cannot. What kind of state Alice sends to these peopel?